Are we blindly accepting all the interpretations that arise from our present description of X-ray diffraction? Is it reasonable that all crystals have to be “ideally imperfect” to determine their structure? Bragg’s law cannot avoid dynamical effects, and therefore the measured intensity is not equal to the square of the structure factor unless the crystal is assumed to be “ideally imperfect”. If polycrystalline diffraction is formed from crystals satisfying Bragg’s law, why is the background so high compared with single crystal profiles? Are more crystals required in polycrystalline diffraction to study complex structures with large unit cells to ensure all the peaks are captured? If the variation of intensity around the diffraction rings from polycrystalline samples is associated with a large range of crystal sizes, why does the data from a standard reference material of similar size crystals still reveal this variation? Are we not just modifying our sample description and instrument performance so that the current theory fits the data? After many years of theoretical and experimental work I am convinced that I have a good explanation.
Let us look back more than a hundred years, when the two Braggs interpreted the experiments of Friedrich, Knipping and Laue. Their interpretation was simple, clever and explained the data giving us Bragg’s law and the Bragg equation. This equation gives the position of the diffraction peaks and any surrounding scattering is considered as a perturbation, giving information on the crystal size, strain and defects. This description struggles to answer the questions above.
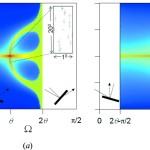
Suppose Bragg’s law is not necessary to form a diffraction peak as proposed by Fewster[1], then we can start to answer these questions. This proposal describes how the specular (mirror) reflections from crystals planes and their periodicity give rise to two peaks, one at the mirror angle and the other at twice the Bragg angle, 2θB. The mirror peak broadens with crystal defects and distortions, with the whole width scattering intensity towards the angle 2θB. This broadened mirror peak contributes to the background[2]. The intensity from crystals not satisfying Bragg’s law will form a weak contribution at the angle 2θB, explaining the intensity variation in diffraction rings from polycrystalline samples. Bragg’s law occurs where the mirror reflection and the angle 2θB peak overlap. Therefore, if the former is broad as in an imperfect crystal Bragg’s law and therefore the dynamical effects can only exist over a small proportion of the intensity profile.
If Bragg’s law is not a requirement to create a diffraction peak, then it is possible for many peaks to be observed simultaneously. This explains the diffraction patterns observed at X-ray free electron lasers, i.e. the appearance of several diffraction spots and their variable intensity. Similarly, the diffraction profiles from polycrystalline materials can be explained, i.e. small numbers of crystals and the full set of peaks from a complex sample. This description accounts for the data but indicates that a typical measurement of intensity close to a diffraction peak is inadequate, because this is only a proportion of the total intensity, and therefore cannot be directly related to the structure factor. A study[1] on a polycrystalline silicon sample suggests that this new description gives the structural parameters within acceptable bounds whereas the conventional theory does not.
The significant step in this description is that the intensity is enhanced at the angle 2θB regardless of the crystal orientation. This can be observed experimentally. So why has it not been knowingly observed before? If conventional theory is so strongly part of the crystallographer’s thinking this enhancement is easy to overlook as just some artifact. This proposal suggests that the derived sample models could be faulty. The magnitude of this error is difficult to assess, but with three components; the diffraction data, a theoretical description and a model of the structure, we require two of these to be correct to reproduce the third. Suppose we assume our data is reliable, then if the theory is incomplete the structural model will be biased or unreliable.
I strongly believe that we should be questioning and discussing our current theory of X-ray diffraction, because all our structural models determined to date might be faulty or inaccurate.
[1] Fewster. (2014). Acta Cryst. A70, 257-282; doi:10.1107/S205327331400117X
[2] Fewster. (2016). Acta Cryst. A72, 50-54; doi:10.1107/S2053273315018975
View the on-demand version of our webinar with Paul Fewster the author of this work on the IUCr YouTube channel.
You can view the questions and answers covered during the webinar here.